Главная » Статьи » Наука и образование

Пары планет земной группы	b	Пары планет  группы планет-гигантов	b
Венера-Меркурий	1,87	Сатурн-Юпитер	1,84
Земля-Венера	1,38	Уран-Сатурн	2,0
Марс-Земля	1,52	Нептун-Уран	1,58

 

Из таблицы видим, что соотношение (b) расстояний соседних пар планет в группах близки к числу два, т.е. они меняется в пределах меньше двух и больше единицы, но не превышает числа два: 

1,4 < b ≤ 2.                                                        (2)

Следовательно, можно предположить, что число два было тем числом, которому были равны соотношения средних расстояний протопланетных поясов в группах,  в которых  аккумулировались группы планет, а пояса формировались между группами как побочный продукт. Из таблицы так же видим, что планеты – гиганты аккумулировались в поясах своей группы более устойчиво, т.к.  они аккумулировались около  средних расстояний своих поясов. Поскольку в работе [6;7;10] получен механизм формирования группы протопланетных поясов  с соотношением их расстояний соответствующих  числу два, и то, что соотношение расстояний сформированных и наблюдаемых планет в группах так же близко к числу два. Таким образом, получен фундаментальный вывод о том, что  планеты Солнечной системы образовались только группами. Они аккумулировались в группах протопланетных поясов, сформированных в околосолнечном диске и имеющих соотношение средних расстояний равное постоянному  числу два Rn+1 / Rn =2 и       
Для сопоставления расстояний планет в группах и средних расстояний протопланетных поясов в группах, построим их числовые модели.Так в  астрономических единицах расстояний планет в группах и указанных в скобках,  средних расстояний пояса астероидов и пояса Койпера, числовая модель   получит вид:
0.373  -   0.72 -   1.0  - 1.5 .. (3.0) …5.2 -  9.5  -  19.2  -  39.5 … (60)… 
Зная, что  соотношения средних расстояний протопланетных поясов равны постоянному  числу два, получим  числовую модель расположения протопланетных поясов в группах и средних расстояний, указанных в скобках, пояса астероидов и пояса Койпера, следующего вида: 
0.25 – 0.5  - 1.0  - 2.0  …(3.0) … 5  - 10 – 20  - 40 …(60)…..  
В модели средние расстояния протопланетных поясов приняты условно, точные их значения не требуется. Они приняты только для показа  соотношения средних расстояний равного постоянному числу два. Из сопоставления расстояний планет и средних расстояний поясов не трудно увидеть, что за время  аккумуляции планет в группе протопланетных поясов их расстояния несколько отклонились от средних расстояний своих поясов, но сохранили основу закономерности  увеличения расстояний протопланетных поясов в наблюдаемой закономерности в увеличения расстояний планет.  Это является не опровержимым фактом, убедительно подтверждающим образование планет группами- аккумуляцией в группах протопланетных поясов, которое имели соотношение  равное числу два:

Rn+1 / Rn =2   (постоянная Солнечной системы)     ( 2 )

Подтверждается и полученный механизм формирования  группы протопланетных поясов, которые имели закономерность  увеличения средних расстояний с соотношением равным числу два. Аккумуляцией планет в группе протопланетных  поясов объясняется, природа групп планет,  наблюдаемая  закономерность увеличения расстояний планет в группах,   и  природа  круговых орбит планет. Таким образом, получено постоянное число два Солнечной системы (постоянная Плеханова), которая и является основой  Закона гармонии.
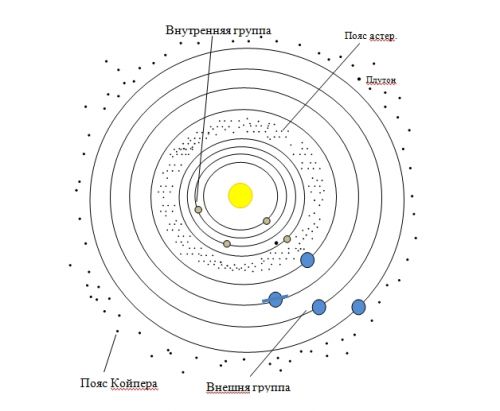
Существование Закона гармонии подтверждается в закономерном расположении групп планет, поясов малых тел между группами, наблюдаемой закономерностью увеличения расстоянии планет в группах и гармоничным строением Солнечной системы (см.Рис.1)
Закон гармонии имеет следующую формулировку: 
«При повороте, согласно эффекта Эйнштейна, вокруг общего полюса - Солнца эллиптических орбит малых тел (комет), с эксцентриситетом (0.5 - 0.6) большая ось одной эллиптической орбиты через каждые 60 градусов в пресечении с  другой орбитой в точках Лагранжа образует четыре радиуса – вектора, которые при дальнейших полных оборотах орбит описывают четыре окружности, радиусы которых имеют соотношение равное числу два (Rn+1 / Rn =2)».

 

 

 

 

 

 

 

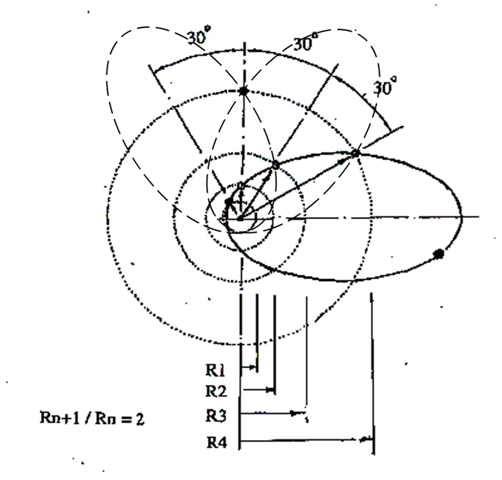
Рисунок 2.  Схема распределения средних  расстояний поясов малых тел - зон аккумуляции группы планет.

 

 

 

 

ЗАКОН ГРУПП
На основании Закона  гармонии ( закона расстояний круговых орбит) получено, что в ранний период эволюции газопылевого диска и формирования планетной системы существовал орбитальный  механизм формирования  вокруг молодого Солнца в его окружающем газопылевом диске   группы из четырех протопланетных поясов   – зон аккумуляции группы планет.  Отсюда следует, что наблюдаемые в Солнечной системе  группы   планет и наблюдаемая группа галилеевых спутников планеты Юпитер  явление не случайное, а  наделено конкретными динамическими и энергетическими  закономерными процессами механизма  формирования группы протопланетных поясов. Механизм основан на неизвестном ранее  свойстве  эллиптических орбит с эксцентриситетом 0.5 множества малых тел (комет) формировать группу  четырех поясов из пыли, газа, малых и более крупных тел, в которых аккумулировалась группа планет. 
Процесс образования группы протопланетных поясов и аккумуляции группы планет показан на Рис.2.  Существование  скоплений  на орбите Юпитера – впереди  его на 60 градусов «Греки»  и позади его на 60 градусов «Троянцы» является наблюдаемым фактом, подтверждающим  образование скоплений в точках Лагранжа (см. Рис. 4). В работе [5;10] установлены скопления, которые расположены в виде «снежинки» на орбите Юпитера и Земли, что также является подтверждающим фактом формирования скоплений. При повороте скоплений вместе с орбитами вокруг Солнца (эффект Эйнштейна)  они   формировали группу из четырех протопланетных поясов, в которых и аккумулировалась группа планет. Механика формирования группы поясов показана на Рис.3. Получено научное определение понятия Закона групп:
«Множество эллиптических орбит  малых тел  обращающихся по эллиптическим орбитам вокруг общего полюса (Солнце) в одной плоскости, при повороте  орбит (эффект Эйнштейна), через каждые 60 градусов в  точках Лагранжа, образуют скопления малых тел, которые при последующих полных оборотах  формируют группу из четырех протопланетных поясов  – зон аккумуляции группы планет».

 

 

 

 

 

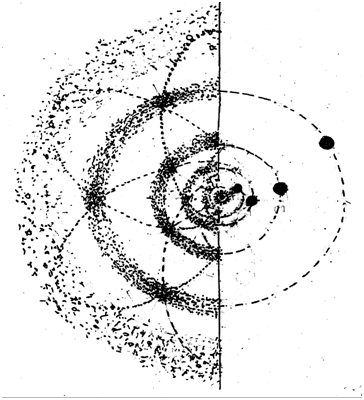
Рисунок 3.   Схема орбитального механизма   формирования группы из четырех
протопланетных поясов –зон аккумуляции группы планет.

 

 

 

 

 

На рисунке видим, что скопления малых тел образуются в точках Лагранжа – местах пересечения  орбит малых тел из которых при последующих  поворотах орбит малых тел (эффект Эйнштейна)  из скоплений формируется группа из четырех протопланетных поясов.

3. ЗАКОН ПОСЛЕДОВАТЕЛЬНОСТИ
Существование короткопериодических комет в зоне внутренней группы планет (с эллиптическими орбитами от Солнца до пояса астероидов) свидетельствует о том, что они являются примером тех  комет которые  в  ранний периоде формировали группу протопланетных поясов, в которых аккумулировались внутренняя группа планет.  Наблюдаемые долгопериодические кометы в зоне группы планет – гигантов  (с орбитами от пояса астероидов до пояса Койпера) так же являются примером тех  комет которые  в  ранний периоде формировали группу протопланетных поясов, в которых аккумулировались внутренняя группа планет. В работе [5]  установлено, что открытый объекта - «Седна» с эллиптической орбитой от пояса Койпера (60а.е.) до расстояния 900 а.е.) является одним из  первых открытых объектов, орбиты которых формировали за пределами пояса Койпера третью группу разряженных протопланетных поясов и третьего пояса. В третьей группе поясов аккумуляция планет не произошла, потому что она сформирована не в зоне околосолнечного диска, а за его пределами. Ближайшие  к Солнцу две группы протопланетных  поясов были плотными, поскольку они были сформированы в околосолнечном газопылевом диске, и поэтому в них аккумулировались группы  планет.   В работе [10]  установлено, что одновременного образования групп протопланетных поясов не наблюдается. Исследованиями установлено, что в начале формировалась долгопериодическими кометами группа из четырех протопланетных поясов, в которой аккумулировалась  внешняя группа  из четырех планет – гигантов. Затем под влиянием тяготения планет – гигантов долгопериодические орбиты малых тел были преобразованы в короткопериодические  орбиты малых тел. Эти короткопериодические  орбиты и формировали группу протопланетных поясов, в которой аккумулировалась  внутренняя группа планет. Пояс астероидов формировался как побочный продукт от последовательного образования групп плане. Последовательность образования групп планет подтверждается тем, группы совершенно разные и то, что астероиды внутренней части пояса отличаются от астероидов внешней его части по химическому составу.   Формулировка закона последовательности:
«За образованием первой (внешней) группы планет следует формирование второй (внутренней) группы планет при этом между группами формируется пояс астероидов, внешняя часть которого формируется процессами образования внешней группы планет, а внутренняя часть (ближе к Солнцу) формируется процессами образования внутренней группы».

Схема преобразования долгопериодических орбит в  короткопериодические орбиты малых тел показана на рисунке 2.

 

 

 

 

 

 

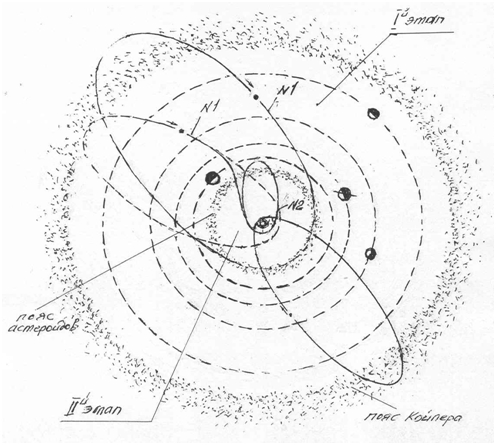
Рисунок 4. Схема образования короткопериодических орбит комет, 
I этап – формирование зоны аккумуляции внешней группы планет
II этап – формирование зоны аккумуляции внутренней группы планет

 

 

 

 

 

На рисунке видно, что внешняя часть пояса астероидов формировалась вместе с группой планет-гигантов Юпитер, Сатурн, Уран и Нептун. При формировании группы протопланетных поясов и аккумуляции в ней внутренней группы планет: Меркурий, Венера, Земля и Марс формировалась внутренняя часть пояса астероидов.   Следовательно, планеты внешней группы  формировали внутреннюю группу планет.    Из механики Закона гармонии, Закона групп и закона последовательности  становится очевидным, что планеты это особый класс небесных тел, которые образовались только группами. Следовательно,  малым телам, астероидам  и объектам поясов не следует присваивать статус малые планеты, карликовые планеты, т.к. это  искажает сущность их происхождения и  природу их существования в Солнечной системе. 

4. ЗАКОН ПОДОБИЯ
Из открытых законов: Закона гармонии (закона расстояний круговых орбит), Закона групп и Закона последовательности следует существование четвертого закона-Закона подобия. Для этого исследованы расстояния группы главных (галилеевых) спутников, которые  обращаются по круговым орбитам вокруг планеты Юпитер. Зная, что соотношения расстояний планет в группах имеют закономерность приближения их значений к числу два проведено сопоставление значений соотношений расстояний планет в группах с  соотношениями расстояний группы главных спутников планеты Юпитер. Если их соотношение будет близким к числу два, то это будет означать, что главные спутники аккумулировались в группе протоспутниковых поясов, которая как и группа планет была сформирована единым механизмом. Это подтвердит, что главные спутники как и планеты образуются группами по четыре спутника в группе. Сопоставление значений соотношения расстояний планет и расстояний группы главных спутников показано в таблице 2.    
Из таблицы видим, среднее значение соотношений группы галилеевых спутников планеты Юпитер (1,646) почти  совпадает со средним значением соотношений расстояний  планет внутренней группы (1,589). Это свидетельствует о том, что спутники образовались группой по подобию образования групп планет. Их группы протоспутниковых поясов были сформированы в околопланетном диске единым орбитальным механизмом. Кольца вокруг планет-гигантов и пояс не регулярных спутников планеты являются остаточным продуктом от образования группы главных спутников. Орбитами каких тел (малых тел, крупных тел или кометами) устанавливается в продолжении исследования малых тел (комет).  
Закон подобия имеет следующую формулировку:
«Группы главных спутников  планет – гигантов аккумулируются в группе протоспутниковых поясов, сформированных единым механизмом формирования протопланетных поясов в которых аккумулировалась группа планет». 

Таблица 2
Сопоставление отношений средних расстояний поясов (b) и соотношений расстояний планет в группах (b)  и соотношений средних расстояний поясов и соотношений расстояний галилеевых спутников

 

Планеты и спутники	R (а. е.)	b (Rn+1/Rn)	R (а. е.)	b (Rn+1/Rn)
Планеты земной группы 1. Меркурий	0,279		0,38
2. Венера	0,558	2	0,723	1.860
3. Земля	1,116	2	1,000	1.383
4. Марс	2,232	2	1,524	1,524
Средние значения (bт) и (bф)  группы		2		1,589
Группа планет-гигантов 1. Юпитер	5,556		5,200
2. Сатурн	11,120	2	9,540	1,835
3. Уран	22,240	2	19,18	2,000
4. Нептун	44,480	2	30,07	1,567
Средние значения (bт) и (bф) группы		2		1,588
Группа галилеевых спутников 1. Ио, тыс.км.	255		422
2. Европа      тыс.км.	510	2	671	1,59
3. Ганимед    тыс.км.	1020	2	1070	1,59
4. Каллисто  тыс.км.	2040	2	1880	1,76
Средние значения (bт) и (bф) группы		2		1,646

 

 

 

 

На основании новых законов небесной механики  получена единая модель строения спутниковых систем планет-гигантов (см. Рис.3). Установлено, что вокруг планеты Сатурн существуют две группы главных спутников. Получены модели строения спутниковых систем у всех планет-гигантов и таблицы их параметров [6].

 

 

 

 

 

 

 

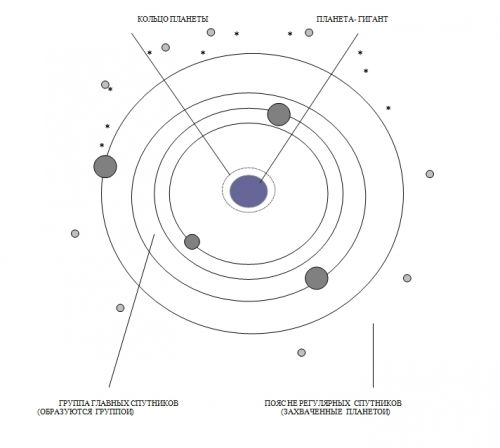
Рисунок 5. Единая модель истинного строения   систем спутников  планет- гигантов:   Юпитер, Сатурн, Уран и Нептун.

 

 

 

 

 

 

 

 

 

 

Рисунок 6. Модель строения всей Солнечной системы

 

 

 

 

 

 

 

 

 

ВЫВОДЫ
В статье впервые в истории астрономии установлено существование четырех законов небесной механики формирования Солнечной системы. На основании новых законов небесной механики получено:
- Планеты и главные спутники планет- гигантов образуются группами.
- Установлена закономерность формирования групп планет, группы главных спутников  планеты Юпитер и пояса астероидов между группами планет.  
- Получено объяснение наблюдаемой закономерности в расстояниях планет в группах.
- Получено объяснение природы круговых орбит планет и главных спутников.
-  Установлена единая модель строения спутниковых систем.
- Установлены группы главных спутников у всех планет - гигантов
- Получена модель строения всей Солнечной системы.
- Установлены группы планет во внесолнечных планетных системах.

Литература:
1. Шмидт О.Ю. Четыре лекции о происхождении Земли /АН СССР  1957

2. Шмидт О.Ю.  О планетных расстояниях / ЛАН СССР, 1944 Том 46, №9

3. Плеханов П.Г.   К вопросу межпланетных расстояний в ранний формирования Солнечной системы - Доклады 53 н/к  СГПУ г.  Самара  1999

4.Плеханов П.Г. Научное определение  понятия  планета (к вопросу о статусе Плутона).- Доклады 55 н/к  Самара, 2001

5.Плеханов П.Г. О существовании «снежинки»  на орбите Земли И планет Солнечной системы. «Естественные науки: актуальные вопросы и тенденции  развития» Материалы международной заочной конференции 30ноября 2011  Новосибирск 2011 -188с.

6.Плеханов П.Г. Механизм формирования группы из четырех поясов – зоны аккумуляции группы планет. Доклады научной конференции СМК выпуск 5 - 2009 год стр. 82-91

7.Плеханов П.Г. О существовании постоянной в соотношениях расстояний планет в группах в ранний период их аккумуляции Доклады 53-й научн. Конференции  СГПУ. Самара, 1999. С. 72-76

8. Плеханов П.Г.– Математическая модель строения Солнечной системы Доклады  56 – й  научной  конф. СГПУ, Самара, 2002

9.Плеханов П.Г. О существовании «снежинки» на орбите Земли и планет Солнечной системы «Актуальные проблемы гуманитарных

10. Плеханов П.Г.  Галлилеевы спутники планеты, не состоявшейся звезды Юпитер.-  Доклады 55 н/к Самара, 2001

11. Плеханов П.Г. Солнечная система XXI века: монография – Самара:  Издательство СГПУ. 2003. – 194 с.

12. Плеханов П.Г.О последовательности образования групп планет Доклады  57 – й  научной  конф. СГПУ, Самара, 2003 С.

13. Плеханов П.Г. Плеханов П.П. О единой модели строения систем спутников планет- гигантов. Доклады  57 – й  научной конференции СГПУ, Самара, 2003 С.

14. Plehanov  P.G.  The original of  the Solar  system: The Monograph.- Samara: LTD PPC   ‘‘Sodruzhestvo’’ – 2006. – 171 pages.