1. ФГБОУ ВПО «Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В.И.Ульянова (Ленина)»
2. ФГБОУ ВПО «Саратовский государственный университет имени Н.Г. Чернышевского»
3. «Физический факультет МГУ им. М.В.Ломоносова»
4. ФГБОУ ВПО «Петрозаводский государственный университет»
Известно, что при исследовании различных линейных и нелинейных спин-волновых явлений в пленочных ферромагнетиках одним из определяющих факторов является закон дисперсии спиновых волн [5, 10]. При изучении свойств МК расчеты, как правило, делаются для структур с бесконечным числом периодов. Теория предсказывает, что спектр собственных состояний f (k) таких структур характеризуется наличием разрешенных зон, соответствующих частотам, на которых возможно распространение спиновых волн, а также запрещенных зон, на частотах которых распространение спиновых волн невозможно. Последние обусловлены брэгговским резонансом. На дисперсионной характеристике запрещенные зоны магнонного кристалла проявляются как разрыв.
Однако в случае магнонных кристаллов, состоящих из ограниченного числа периодов, вместо запрещенных зон имеют место зоны с относительно высоким затуханием СВ. Несмотря на то, что в таких зонах коэффициент передачи СВ сравнительно мал, тем не менее в них имеет место распространение волн. Поэтому частотная зависимость коэффициента передачи спиновых волн (амплитудно-частотная характеристика) магнонного кристалла конечной длины характеризуется чередованием полос пропускания с малыми и большими потерями. Последние в дальнейшем будем называть “полосами заграждения”.
Несмотря на разнообразие существующих подходов [1–4,7–9] к описанию свойств магнонных кристаллов, детальное теоретическое изучение распространения спиновых волн в них проводилось только для случая бесконечных периодических магнитных структур. Целью настоящей работы являлось теоретическое исследование характеристик передачи магнитных микро- и наноструктур методом волновых матриц передачи, который учитывает особенности распространения спиновых волн в образцах конечных размеров.
В качестве объекта исследования нами была выбрана структура, представлявшая собой монокристаллический волновод из пленки железо-иттриевого граната, содержащий неоднородности в виде периодической системы канавок. Схематическое изображение исследовавшейся структуры показано на рисунке 1. Для такого объекта исследования все волноведущие свойства определяются в основном геометрией структуры и свойствами ферромагнитной пленки.
При дальнейшем расчете будем полагать, что канавки ориентированы строго перпендикулярно направлению распространения спиновых волн. Внешнее поле подмагничивания направлено в плоскости пленки вдоль канавок. Такая взаимная конфигурация направления распространения и ориентации поля подмагничивания будет соответствовать распространению поверхностных спиновых волн в одномерном магнонном кристалле.

Рассмотрим способ описания волноведущих свойств магнонных кристаллов при помощи аппарата волновых матриц передачи. Волновую матрицу передачи, описывающую распространение спиновых волн через одну секцию вышеописанной периодической структуры (состоящей из участков пленки различных толщин), можно представить в виде последовательного перемножения четырех отдельных матриц:
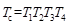 . (1)
. (1)
Здесь каждая матрица отвечает за свой участок волноведущей структуры, а именно: матрица T1 учитывает распространение волны на участке пленки ЖИГ с большей толщиной; матрица T2 учитывает отражение спиновой волны от границы раздела “толстая”/“тонкая” пленка; матрица T3 учитывает распространение волны на участке пленки меньшей толщины; матрица T4 учитывает отражение от границы раздела “тонкая”/“толстая” пленка. Результирующее выражение (1) можно записать как
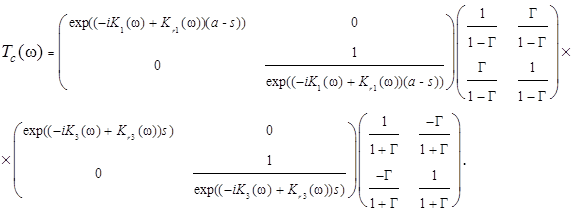 (2)
(2)
В формуле (2) использованы следующие обозначения: K1(ω), K3(ω) и Kr1(ω), Kr3(ω) – волновые числа и пространственные коэффициенты затухания, соответственно, для “толстого” и “тонкого” участков пленки; Γ – коэффициент отражения; a – период структуры; s – ширина канавок.
Обычно при решении задач о дисперсии спиновых волн в периодических пленочных магнитных структурах используются различные приближения. Самыми распространенными среди них являются магнитостатическое (длинноволновое) приближение, когда учитывается только диполь-дипольное взаимодействие спиновых волн, а также обменное (коротковолновое) приближение, когда в уравнении движения намагниченности оставляют слагаемые, описывающие только неоднородное обменное взаимодействие спиновых волн, пренебрегая их диполь-дипольным взаимодействием. В данной работе дисперсионные характеристики волноведущей структуры рассчитываются только с учетом диполь-дипольного взаимодействия. Выбор такого приближения обусловлен тем, что экспериментальное изучение линейных и нелинейных эффектов в ферромагнитных структурах при обмененном взаимодействии сильно затруднено. В нулевом приближении теории возмущений в случае свободных поверхностных спинов спектр поверхностных спиновых волн имеет вид
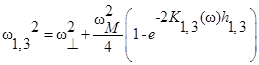 (3)
(3)
где h1,3 – толщины пленок ферромагнетика в МК. Коэффициент затухания СВ определяется как
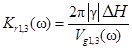 (4)
(4)
где ΔH – полуширина линии ферромагнитного резонанса; Vg1,3(ω) – групповая скорость СВ, получаемая путем дифференцирования дисперсионного уравнения (3).
Итоговая волновая матрица для периодической структуры, состоящей из n периодов, получается путем перемножения n матриц передачи отдельных периодов
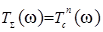 , (5)
, (5)
при этом коэффициент передачи магнонного кристалла (в децибелах) равен
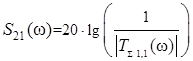 . (6)
. (6)
Важно отметить, что положение полос заграждения в частотном спектре зависит от геометрии периодической структуры, материалов, из которых она изготовлена, величины и направления внешнего поля подмагничивания. Параметры моделируемых структур были выбраны из тех соображений, что на участке дисперсионной характеристики, определяемой диполь-дипольным механизмом распространения спиновых волн, должно располагаться несколько полос заграждения, обусловленных брэгговским отражением (бриллюэновским рассеянием) спиновых волн. Исследовавшаяся структура имела период a = 400 мкм, ширину s и глубину Δ канавок 50 и 2 мкм соответственно, толщина толстой области h1 равна 12 мкм. Величина коэффициента отражения полагалась равной 0,13. При расчете полагалось, что намагниченность насыщения феррита составляла 1750 Гс.
Теоретическое исследование проводилось в несколько этапов. Вначале исследовалось влияние длины периодической структуры на ее передаточную характеристику и закон дисперсии спиновых волн. Под длиной магнонного кристалла понималась величина d = a·n. Поскольку для приведенных далее расчетов период структуры был фиксированным, то сравнивались структуры, состоящие из различного числа периодов. Расчет производился для идеального случая, когда полуширина линии ферромагнитного резонанса и, соответственно, декременты затухания спиновых волн Kr1,3(ω) в магнонном кристалле полагались равными нулю.
На рис. 2 представлены результаты численного моделирования влияния длины одномерного магнонного кристалла на его передаточную и дисперсионную характеристики. На вставках на рис. 2 показаны в увеличенном масштабе участки передаточных и дисперсионных характеристик, соответствующие полосам заграждения магнонного кристалла. Кривые 1 на рис. 2 соответствуют случаю структуры, состоящей из одного периода. Как видно из рисунка, при n=1 вносимое затухание при распространении спиновой волны на всех частотах относительно невелико, а дисперсионная характеристика подобна дисперсионной характеристике однородной пленки ЖИГ. Кривые 2 и 3 построены для структур, состоящих из 15 и 1000 периодов соответственно.
Вид приведенных кривых можно объяснить следующим образом. Вне полос заграждения, когда набег фазы за период K1(a–s)+K2s≠π (условие эффективного брэгговского резонанса), эффективного отражения спиновых волн от периодической структуры не происходит, и результирующий набег фазы пропорционален расстоянию, пробегаемому волной. В этом случае в спектре МК наблюдается полоса пропускания, а дисперсионная характеристика МК подобна дисперсионной характеристике однородной пленки феррита.
В случае распространения в МК спиновых волн, имеющих несущие частоты вблизи полос заграждения, наряду с дисперсией среды определенную роль играет дисперсия, обусловленная периодичностью структуры. В случае, если условие Брэгга выполняется приблизительно K1(a–s)+K2s≈π, волна испытывает брэгговское отражение и по мере распространения в периодической структуре затухает, передавая энергию отраженным волнам. В этой режиме волновое число спиновой волны является комплексным [6].
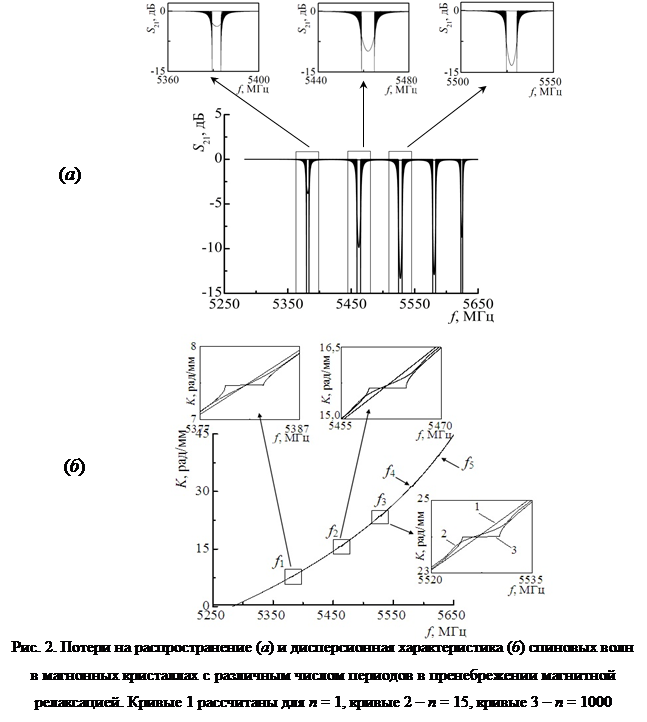
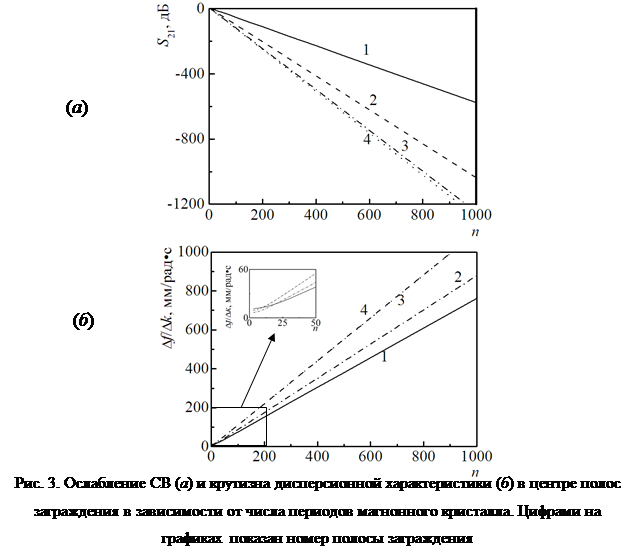
В случае бесконечного МК падающая волна должна полностью отразиться на частотах брэгговского резонанса. На частотном коэффициенте передачи бесконечного магнонного кристалла этот факт должен проявляться в виде запрещенных зон, распространение спиновых волн на которых невозможно. Однако, как видно из рисунка 2, в случае МК конечной длины на передаточной характеристике вместо запрещенных зон имеют место зоны с относительно большими, но конечными вносимыми потерями – полосы заграждения. По мере увеличения длины магнитной периодической структуры увеличиваются и потери внутри полосы заграждения МК, по закону e-k”d, где k” – декремент затухания внутри полосы заграждения. Зависимости вносимых в полосе заграждения потерь от длины периодической структуры для первых четырех полос заграждения в логарифмическом масштабе представлены на рисунке 3 (а).
Отметим, что переотраженные периодической структурой волны вносят существенный вклад в формирование фазочастотной и, как следствие, дисперсионной характеристик магнонного кристалла. При этом на дисперсионной характеристике полосы заграждения конечного магнонного кристалла проявляются как участки “перегиба”, имеющие свою зависимость f от k, отличную от дисперсионной зависимости свободной пленки ЖИГ (рисунок 2 (б)).
Увеличение числа периодов приводит к тому, что эти участки “перегиба” меняют свою крутизну ∆f/∆k (см. вставки на рис. 2 (б) и рис. 3 (б)). Так, например, при n = 1 угол наклона дисперсионной характеристики внутри полосы заграждения соответствует углу наклона дисперсионной характеристики однородной пленки ЖИГ, и ∆f/∆k составляет 8 мм/рад·с. При n = 1000 зависимость f(k) идет с наклоном ∆f/∆k порядка 1000 мм/рад·с (при выбранных параметрах теоретического расчета) и подобна дисперсионным характеристикам, соответствующим бесконечным периодическим структурам, представленным, например, в [8].
Таким образом, исследование показало, что на длине пути, равном конечному числу периодов магнонного кристалла, вблизи частот брэгговских резонансов спиновые волны распространяются, испытывая более сильное затухание, чем в других областях спектра. Крутизна дисперсионной характеристики в полосах заграждения зависит от протяженности магнонного кристалла.
Работа выполнена при поддержке Министерства образования и науки России Федеральными программами «Научные и педагогические кадры инновационной России" и "Развитие потенциала высшей школы".
Рецензенты:
Головков Александр Алексеевич, д.т.н., профессор, профессор кафедры «Радиоэлектронных средств» ФГБОУ ВПО «Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В. И.Ульянова (Ленина)» Минобрнауки России, г. Санкт-Петербург.
Баранов Игорь Владимирович, д.т.н., профессор, заведующий кафедрой «Физика ИХиБТ», заместитель директора института холода и биотехнологий ФГБОУ ВПО «Санкт-Петербургский национальный исследовательский университет информационных технологий механики и оптики» Минобрнауки России, г. Санкт-Петербург.
Пристатейные списки литературы
1. Бегинин Е. Н. Электродинамические характеристики периодических и фрактальных волноведущих микроструктур на основе ферритовых пленок / Е. Н. Бегинин, С. В. Гришин, Ю. П. Шараевский и др. // Гетеромагнитная электроника. – 2011. – Вып. 9. – С.16-28.
2. Вороненко А. В. Дифракция поверхностных магнитостатических волн на магнитных решетках в режиме Брэгга / А. В. Вороненко, С. В. Герус, В. Д. Харитонов // Известия вузов. Физика. – 1988. – Т. 31. – Вып. 11. – С. 76 – 85.
3. Григорьева Н. Ю. Дисперсионные характеристики спиновых волн в планарных периодических структурах на основе ферромагнитных пленок / Н. Ю. Григорьева, Б. А. Калиникос // ЖТФ. – 2009. – Т. 79, Вып. 8. – С. 110-117.
4. Локк Э. Г. Дисперсия магнитостатических волн в композитной структуре феррит – решетка металлических полосок / Радиотехника и электроника. – 2003. – Т. 48, № 12. – С. 1484–1494.
5. Устинов А. Б. Наблюдение солитонов огибающей спиновых волн в периодических магнитных пленочных структурах / А. Б. Устинов, Н. Ю. Григорьева, Б. А. Калиникос // Письма в ЖЭТФ. – 2008. – Т. 88. – В. 1. – С. 34-39.
6. Ярив А. Оптические волны в кристаллах / А. Ярив, П. Юх. – М.: МИР, 1987. – 616 c.
7. Chumak A. V. Design and optimization of one-dimensional ferrite-film based magnonic crystals / A. V. Chumak, A. A. Serga, S. Wolff, // J. Appl. Phys. – 2009. – Vol. 105, Issue 8. – P. 083906.
8. Elachi C. Waves in active and passive periodic structures: a review / Proceedings of the IEEE, – 1976. – Vol. 64, № 12. – P. 1666-1698.
9. Sykes C. G. Magnetostatic wave propagation in a periodic structure / C.G. Sykes, J.D. Adam, J.Н. Collins // Appl. Phys. Lett. – 1976. – Vol. 29, №6. – P. 388-391.
10. Ustinov A. B. Observation of the chaotic spin-wave soliton trains in magnetic films / A. B. Ustinov, V. E. Demidov, A. V. Kondrashov, B. A. Kalinikos, S. O. Demokritov // Phys. Rev. Lett., – 2011. – V. 106. – I. 1. – P. 017201.